Relations and Functions NCERT Solutions

NCERT Exercise 1.1 Q: 2 - 9

Question:2: Show that the relation R in the set R of real numbers, defined as R = {(a, b):a ≤ b²} is neither reflexive nor symmetric nor transitive.

Solution:

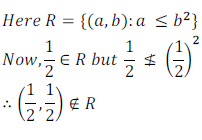
So, R is not a reflexive relation.

Let, (2, 9) ∈ R then (9, 2) ∉ R because 9 is not less than or equal to 2²

So, R is not symmetric relation.

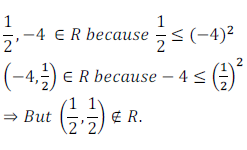
So, R is not transitive relation.

Thus, R is neither reflexive nor symmetric nor transitive.

Question: 3. Check whether he relation R defined in the set {1, 2, 3, 4, 5, 6} as R = {(a, b): b = a + 1} is reflexive, symmetric or transitive.

Solution:

Hare A= {1, 2, 3, 4, 5, 6}

R= {(a, b): b = a + 1}

= {(1, 2), (2, 3), (3, 4), (4, 5), (5, 6)}

Now, 1, 2, 3, 4, 5, 6 ∈ A

But, (1, 1), (2, 2), (3, 3), (4, 4), (5, 5) (6, 6) ∉ R

So R is not reflecxive relation.

(1, 2)∈R but (2, 1) ∉ R

So, R is not symmetric relation.

( 3, 4) ∈ R and (4, 5)∈ R but (3, 5) ∉ R

So, R is not transitive relation.

Thus R is neither reflexive nor symmetric nor transitive.

Question: 4. Show that the relation R in R defined as R = {(a, b):a ≤ b} is reflexive and transitive but not symmetric.

Solution:

Here, R = {(a, b):a ≤ b}

Let, b = a than (a, b) ∈ R because a&le, b.

So, R is reflexive relation.

Let, (a, b) ∈ R ⇒ a ≤ b

⇒ (b, a) ∉ R since both a ≤ b and b ≤ a

Can't hold true together.

So, R is not symmetric relation.

Let, (a, b) ∈ R and(b, c) ∈ R

⇒ a ≤ b and b ≤ c

⇒ a ≤ c

⇒ (a, c) ∈ R.

So, R is transitive relation.

Thus, R is reflexive and transitive but not symmetric.

Question: 5. Check whether the relation R in R defined by

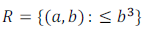is reflective, symmetric or transitive.

Solution: Here,

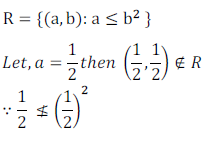
So, R is not reflexive relation.

Let, (1, 2) ∈ R then (2, 1) ∉ R because 2 is not less than equal to 1³ .

So, R is not symmetric relation.

Let, (9, 3) ∈ R then (3, 2) ∈ R then (9, 2) ∈ R because 9 is not less than equal to (2)³

So, R is not transitive relation.

Thus, R is neither reflexive nor symmetric nor transitive.

Question: 6. Show that the relation R in the set {1, 2, 3} given by R = {(1, 2), (2, 1)} is symmetric but neither reflexive nor transitive.

Solution:

Let, A = {1, 2, 3}

R = {(1, 2), (2, 1)}

Now, 1 ∈A but (1, 1) ∉ R.

So, R is not reflexive relation.

(1,2)∈ R and (2, 1)∈ R.

So, R is symmetric relation.

(1, 2) ∈ R and (2, 1)∉ R but (1,1) ∉ R

So, R is not transitive relation.

Thus, R is symmetric but neither reflexive nor transitive.

Question: 7. Show that the relation R in the set A of all the books in library of a college given by R {(x, y): x and y have same number of pages} is an equivalence relation.

Solution:

Here, R = {( x, y): x and y have same number of pages}

Now obviously,

Therefore, (x, x) ∈ R

So, R is reflexive relation.

(x, y)∈ R⇒ (y, x) ∈R because number of pages in both the boxes is same

So, R is symmetric relation.

(x, y)∈ R and (y, z)∈ R

⇒(x, z) ∈ R because number of pages in book x and z is same

So, R is transitive relation

So, R is the reflective, symmetric and transitive.

Thus, R is an equivalence relation.

Question: 8. Show that the relation R in the set A = {1, 2, 3, 4, 5} given by R = {(a, b): |a –b| is even} is an equivalence relation. Show that all the elements of {1, 3, 5} are related to each other and all the elements of {2, 4} are related to each other. But no element of {1, 3, 5} is related to any element of {2, 4}.

Solution:

Here, A {1, 2, 3, 4 5}

R = {(a, b): |a – b| is even}

= {(1, 1), (1, 3), (1, 5), (2, 2), (2, 4), (3, 1), (3, 3), (3, 5), (4, 2), (4, 4), (5, 1), (5, 3), (5,5)}

Now, 1, 2, 3, 4, 5, ∈ A ⇒ (1, 1), (2, 2), (3, 3), (4, 4), (5, 5) ∈ R

Also |a - a|= 0 which is even

⇒ (a, a )∈ R

So, R is reflective relation.

If |a – b|is even, |b – a |is also even.

So, (a, b) ∈ R ⇒ (b,a) isin R

So, R is symmetric relation.

If (a, b ) ∈R and (b, c) ∈ R

⇒ |a - b|is even and |b - c|is even.

Say a – b = 2k₁

And b – c = 2k₂

Where, k₁ and k₂ are integers.

Then a – c =(a – b) + (b – c)

2k₁ + 2k₂

⇒ 2 (k₁ + k₂)

⇒ | a – c | is even.

⇒ (a, c)∈ R

So, R is transitive relation.

Now, the elements of {1, 3, 5} are related to each other because

|1 – 3 |= 2; |3 – 5| = 2, |1 - 5|= 4

All numbers are even numbers.

The elements of {2, 4} are related to each other because |2 – 4 |= 2, which is even number.

No elements of set {1, 3, 5} is related to any element of {2, 4} because |1 – 2 |= 1; |3 - 2|=1; |5 – 2 |= 3; |1 - 4|= 3; |3 -4 | = 1; |5 - 4|= 1 Which are not even numbers.

Question: 9. Show that each of the relations R in the set A = {x ∈ Z;0 ≤ x ≤ 12} given by

(i)R = { ( a, b) ; |a –b| is a multiple of 4 }

(ii) R = {(a, b): a = b}

Is an equivalence relation, find the set of all elements related to 1 in each case.

Solution:

Here A = {x ∈ Z; 0 ≤ x ≤ 12}

= {o, 1, 2, 3, ------, 12}

(i) R = {(a, b):|a - b|is a multiple of 4}

= {(0, 0), (0, 4), (0, 8), (0, 12), (1, 1), (1, 5), (1, 9), (2, 2) (2, 6), (2, 10), (3, 3),(3, 7), (3, 11), (4, 4), (4, 8), (4, 12), (5, 5), (5, 9), (6, 6) (6, 10 ), (7, 7), (7, 11), (8, 8), (8, 12), (9, 9), (10, 10), (11, 11), (12, 12)}

Now 0, 1, 2, 3, -----, 12∈ A

Then, (0, 0), (1, 1), (2, 2), -------- (12, 12)∈ R

So, R is a reflexive relation.

(1, 5) ∈ R then, (5, 1) ∈ R because |5 – 1|= |1 – 5|.

So, R is symmetric relation.

(2, 6) ∈ R and (6, 10) ∈ R then (2, 10) ∈ R because |2 – 10 |= 8 which is multiple of 4 .

So, R is transitive relation.

Thus, R is an equivalence relation.

The set of elements related to 1 is {1, 5, 9}.

(ii) R = {(a, b) : a = b} = {( 0, 0), (1, 1) (2, 2), -----, (12, 12)}

Now, 0, 1, 2, 3, ---- 12 ∈ A then (0, 0), (1, 1), (2, 2), ----, (12, 12) ∈ R

So, R is a reflexive relation.

(2, 2) ∈R then (2, 2) ∈ R

So, R is symmetric relation.

(5, 5) ∈ R and (5, 5) ∈ then (5, 5) ∈ R

So, R is transitive relation.

Thus, R is an equivalence relation.

The set of elements related to 1 is {1}.

12-math-home

Reference: