Relations and Functions NCERT Solutions

NCERT Exercise 1.2

Question: 1. Show that the function f: R_* → R_* defined by F(x) = 1/x is one- one and onto, Where R_* is the set of all non- zero real numbers. Is the result true, if the domain R_* is replaced by N with co- domain being same as R_*?

Solution:

Let x₁ ≠ 0 and x₂≠ 0 ∈ R_*

Here f(x) = 1/x Then,

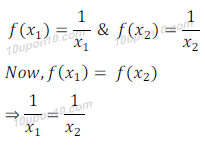
⇒ x₁= x₂

So f is one - one function.

Let f(x) = 1/x = y ≠ 0 ∈ R_* ( codomain of f)

⇒ x = 1/y ∈ R_* ( domain of f)

So, f is onto function.

When domain R_* is replaced by N and codomain remains same then f:N →R

Let x₁, x₂ ∈ N

Then,

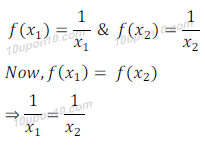
⇒ x₁= x₂

So, f is one- one function.

But every real number belonging to co–domain may not have a pre image in domain of natural numbers.

Here 3/5 ∈ R

But 1/3 = 5/3 ∉ N

So,f is not onto function.

Question: 2. Check the injectivity and surjectivity of the following functions:

(i) f:N → N given by f(x) = x²

(ii) f:Z → Z given by f(x) = x²

(iii) f : R → R given by f(x) = x²

(iv) f : N →N given by f(x) = x³

(v) f: Z → Z given by f(x) = x³

Solution:

(i) Here f (x) = x²

Let x₁, x₂ ∈ N then

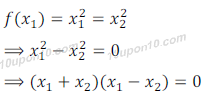
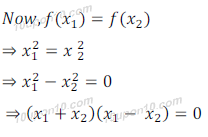
Since, x₁, x₂ ∈ N

So, x₁ + x₂ = 0 is not possible.

∴ , x₁ – x₂ = 0

⇒ x₁ = x₂

∴ f (x₁) = f(x₂) ⇒ x₁ = x₂

So, f is injective function.

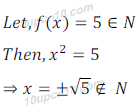
So, f is not surjective function.

(ii) Here f(x) = x²

Let, x₁, x₂ and x₂ = – 3 ∈ Z

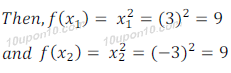
Therefore, f (x₁) = f(x₂) but x₁ ≠ x₂

So, f is not injective function.

Let f(x) = 5 ∈ Z

∴ x^{2 = 5 ⇒ x ≠ √5 ∉ Z}

So, f is not surjective function.

(iii) Here f (x) = x²

Let, x₁ = 4 ∈ R

And x₂ = – 4 ∈ R

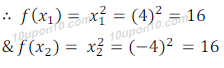
∴ f(x₁) = f (x₂)

but x₁ ≠ x₂

So, f is not injective function.

Let f(x) = – 3 ∈ R

∴ x² = – 3 ⇒ x = ± √ – 3 ∉ R

So, f is not surjective function.

(iv) Here f(x) = x³

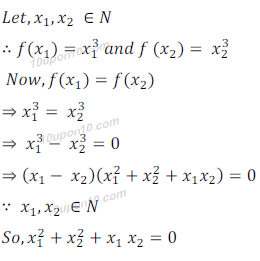
Which is not possible.

∴ x₁ – x₂ = 0

⇒ x₁ = x₂

∴ f(x₁) = f(x₂)

⇒ (x₁) = (x₂)

So, f is injective function.

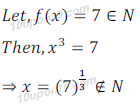
So, f is not surjective function.

(v) Here f(x) = x³

Let, x₁, x₂ ∈ N

Then,

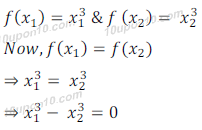
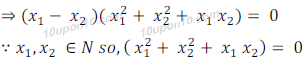
Which is not possible.

∴ x₁ – x₂ = 0

⇒ x₁ = x₂

∴ f(x₁ = f(x₂)

So, f is injective function.

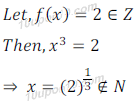
So, f is not surjective function.

Question: 3. Prove that the Greatest Integer Function f: R→R, given by f(x) = [x], is neither one-one nor onto, where [x] denotes the greatest integer less than or equal to x.

Solution:

Let x₁ = 3.5 and

x₂ = 3.2 ∈ R;

Here f (x) =[x]

Then, f(x₁) =[3.5] = 3

and f (x₂) = [3.2] = 3

Now f(x₁) = f(x₂)

But x₁ ≠ x₂

So, f is not one - one function.

Let f(x) = 2.2 ∈ R

Then [x] = 2.5 which is not possible because there is no value of x corresponding to which [x] = 2.5.

So, f is not onto function.

Thus f is neither one-one nor onto function.

Question: 4. Show that the Modulus Function f: R → R given by f(x) = |x| is neither one-one nor onto, were |x| is x, if x is positive or 0 and |x| is –x if x is negative.

Solution:

Let x₁ = 2 and x₂ = –2 ∈ R

Here f(x)=|x|

Then f(x₁) =|2| = 2 and

f(x₂) = |–2| = 2

Now f(x₁) = f (x₂)

but x₁ ≠ x₂

So, f is not one-one function.

Thus f is neither one-one nor onto function.

Question: 5. Show that the Singnum function f:R → R given by 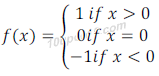is neither one-one nor onto.

Solution:

Let x₁ = 2 > 0 and x₂ = 3 > 0 ∈ R

Then f(x₁) = f (2) = 1 and f(x₂) = f (3) = 1

Now f(x₁) = f ( x₂) but x₁ ≠ x₂

So, f is not one-one function.

There is no value of x for which f(x) = 3 because range of f is |–1, 0, 1|

So, f is not onto function.

Thus f is neither one-one nor onto function.

12-math-home

Reference: