Light: Reflection & Refraction - Class 10th Science
Sign convention for Spherical Lenses
Sign conventions for spherical lens are similar to spherical mirror.
Set of sign convention of reflection by spherical mirror is called New Cartesian Sign Convention also.
Rules of New Cartesian Sign Convention
The pole (P) of the mirror is taken as origin. The principal axis of the lens is taken as the x–axis of the coordinate system. The conventions are as follows:
(i) The object is always placed to the left of the lens. This implies that the light from the object falls on the lens from the left hand side.
(ii) All distances parallel to the principal axis are measured from the pole of the lens.
(iii) All the distances measured to the right of the origin (along + x–axis) are taken as positive while those measured to the left of the origin (along – x–axis) are taken as negative.
(iv) Distances measured perpendicular to and above the principal axis (along + y–axis) are taken as positive.
(v) Distances measured perpendicular to and below the principal axis (along – y–axis) are taken as negative.
Lens Formula and Magnification
Lens formula gives the relationship between distance of object (u), distance of image (v) and focal length (f).
Lens formula tells that reciprocal of focal length is equal to the reciprocal of distance of image minus reciprocal of distance of object. This can be expressed as follows:
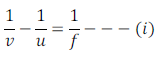
Expression (i) is known as the lens formula. This lens formula is valid in all situations for any spherical lens.
Magnification
The magnification produced by a spherical lens is given by the ratio of height of image to the height of object. Magnification is generally denoted by letter 'm'.
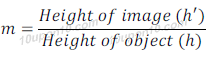
Magnification (m) produced by a spherical lens is related to distance of image and distance of object too.
Thus,
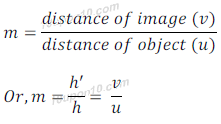
Power of Lens
The ability to converge or diverge rays of light depends on the focal length of a spherical lens. The ability of converge or diverge rays of light is indirectly proportional to the focal length.
This means a lens with greater focal length has less converging or diverging ability of rays of light.
Example: A convex lens of short focal length bends the light rays through large angles by focusing them closer to the optical centre. Similarly, a concave lens of very short focal length causes higher divergence than one with longer focal length.
The degree of convergence or divergence of light rays achieved by a lens is expressed in terms of its power.
Since, ability to convergence or divergence of a lens depends on the focal length of a lens, and ability to convergence of divergence is called the power of lens. Thus, power of a lens is related to the focal length of a lens.
The power of a lens is denoted by letter 'P'.
The power of a lens is the reciprocal of its focal length.
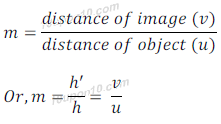
The SI unit of power of a lens is 'dioptre' and is denoted by letter 'D'.
If focal length (f) of a lens is denoted in meter (m), then power of the lens is denoted by dioptres.
1 dipotre is the power of a lens whose focal length is 1 meter.
Thus, 1D = 1m–
Negative and Positive Power of a lens
Power of a Convex lens is expressed with positive sign (+) and power of a Concave lens is expressed with negative (–) sign.
Example: If a doctor prescribed a spectacle with power of glass equal to +1 dioptre, this means the lens is convex.
And if the power of prescribed lens of spectacle is equal to –2 dipotre, this means the lens is concave.
The net Power
Optical instruments, such as a high quality telescope, consist of number of lenses. Many lenses are combined to increase the magnification and sharpness of image.
If there are four lenses having power of P1, P2, P3, and P4 are in contact in an optical instrument,
Then net power of lens (P) = P1 + P2 + P3 + P4
How power of lens is prescribed by an optician
While testing the eye, if an optician found, the two lenses with power of 2.00 D and 0.25 D is suitable for a patient with eye problem.
Then, net power (P) of the lens = 2.00 D + 0.25 D = 2.25 D
Thus, optician prescribes a power of 2.25 D to the patient.